微積分的力量-讀書筆記
首先,我想說的是我為什麼要分享這本書呢?因為這是一本寫給每個人的微積分科普讀物,是被名字耽誤的寶藏趣味科普,它可能會讓你愛上數學。我們知道從宇宙的終極謎題到日常的衣食住行,微積分的力量無處不在。我們現代社會的種種方便——GPS、微波爐、激光視力矯正手術、高鐵等等,都依賴於微積分的發明。沒有微積分,這些事情都無法實現。那微積分對我們的日常生活產生了怎樣的深遠影響呢?如何利用其預測能力去重構世界?本書帶你透過數學語言讀懂世界。
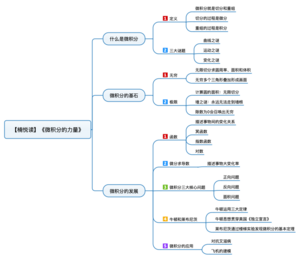
什麼是微積分
有一種罕見而有趣的歷史觀點認為,世界被一個神秘的數學分支徹底改變了。一個最初與形狀相關的理論,最終又如何重塑了文明?我們可以從物理學家理查德·費曼的一句妙語中洞見這個問題的答案,這句話是他在與小說家赫爾曼·沃克討論曼哈頓計劃時說的。
當時沃克正在為他計劃寫作的一部關於「二戰」的長篇小說做調研,他去加州理工學院採訪了參與過原子彈研發的物理學家,費曼就是其中之一。採訪結束臨別之際,費曼問沃克是否了解微積分。沃克坦承他並不了解,於是費曼說道:「你最好學學微積分,它是上帝的語言。」費曼的評價是相當高的。那什麼是微積分?
定義
簡言之,微積分就是想讓複雜的難題簡單化,它十分痴迷於簡單性。微積分成功的方法是,把複雜的問題分解成多個更簡單的部分。當然,這種策略並不是微積分獨有的。所有善於解決問題的人都知道,當難題被分解後,就會變得更容易解決。
微積分真正不同凡響和標新立異的做法在於,它把這種分而治之的策略發揮到了極致,也就是無窮的程度。比如,杯子的形狀,不是一個簡單的形狀,它很複雜。如果我們只用簡單的平面幾何、立體幾何,是無法計算清楚的。但是微積分可以把它簡單化。
比如,請問圓是怎麼算出來的?這是幾何學的知識。我們都知道周長,比如我做一個比薩,我拿一根繩子繞着它這麼轉一圈,然後把這個繩子拿出來一量,就知道這個圓的周長了。那怎麼測量這個圓的面積呢?不能用繩子去測量圓的面積,我們需要的是圓的面積公式。
周長的公式是π×d。πd是怎麼算出來的呢?把周長測出來,然後把直徑測出來,用周長除以直徑,得到的數就是π,所以π就是圓周率。那你有沒有想過為什麼面積會是πr²,而不是πd²?這就是微積分的思想。
你想象這是一個圓,我想知道它的面積,怎麼辦呢?你想象像切西瓜一樣,沿着它的中心,切成一牙一牙的西瓜。然後你把它掰開,上半截就變成了一個向下的鋸齒,下半截就變成了一個向上的鋸齒。然後你把上半截和下半截對在一塊兒,成了一個什麼形狀呢?類似於一個長方形。但是這個長方形的上邊不是一條直線,而是一個一個的弧度。那假如你把這個西瓜切到非常薄,薄到極限,那個弧度是不是就變成了一個一個的點?用弧度構成的這條邊,是不是就變成了一條趨近於直線的東西?
這時候你發現,圓如果可以被切到無窮塊,那它將會成為一個相當標準的矩形。請問這個矩形的高是多少呢?是半徑。那個長的一邊呢?是二分之一個周長,也就是πd÷2。πd÷2不就是πr嗎?再乘以半徑,得出是πr²。現在大家知道πr²是怎麼來的了嗎?就是通過切分想象出來的。所以古人能通過切分到無窮的程度,想象出來這麼一個構造,解決了測量圓面積的問題,這就是微積分的思想。所以微積分的實質就是切分和重組,切分的過程叫微分,重組在一起叫積分。
因為古希臘人特別喜歡研究數學,所以到了公元前250年左右,他們都在研究數學。在那個時候他們就已經有了微積分的思想,所以微積分不是一件很可怕的事,微積分最主要的應用就是解決三大謎題。
三大謎題
首先,曲線之謎。就是我們說圓形怎麼算?弧形怎麼算?拋物線怎麼算?那請問一條拋物線拋出去,你會不會算拋物線下邊的面積?這在微積分中是最簡單的一道題。給你一個拋物線的公式,就能算出拋物線底下的面積,這叫曲線之謎。
其次,運動之謎。世界上的勻速直線運動幾乎沒有,你不可能見到哪個人是一直保持勻速直線運動的,他一定會有加速和減速的過程。如果運動之謎解決不了,你的炮彈打得就不准,就無法準確地計算這個炮彈落下去在哪兒,所以這跟軍事是有關的。
最後,變化之謎。比如你體內的細胞增長了、減少了,這個變化的速率是不均勻的,所以用簡單的加減乘除根本無法計算。所以曲線之謎、運動之謎和變化之謎,跟我們的生活息息相關。沒有微積分這樣的工具,我們就無從了解。
微積分的基石
接下來我們說說,微積分的基石,極限和無窮的應用。
無窮
作者說,我們要知道無窮的魅力和危險。
比如,芝諾悖論。芝諾說,烏龜比阿喀琉斯先出發1米,然後讓阿喀琉斯去追烏龜,結論是阿喀琉斯永遠追不上烏龜。為什麼呢?他說在烏龜往前走一點的過程中,需要一個時間;阿喀琉斯追它也需要一個時間。當阿喀琉斯走到烏龜原來的位置,在相同時間內,烏龜也往前挪了一點點。在下一個時間段,當阿喀琉斯又走到烏龜原來的位置,在相同時間內,烏龜又往前挪了一點點。所以阿喀琉斯永遠追不上烏龜。
有道理嗎?有數學家解釋說,你不知道極限嗎?烏龜每次走得少一點,少一點,少一點,最後加在一起,不會超過1。
極限
阿喀琉斯論證說,你朝一面牆走,每次走1/2,永遠走不到那面牆跟前。為什麼呢?因為你要走到那兒去,必然走過中間的一半,你走過這個一半以後,必然得走過那個中間的一半,也就是1/4的地方。然後你得再走過1/8的地方、1/16的地方、1/32的地方……你永遠都得走過你和這個牆中間距離的一半的位置。 所以就算再小,你和牆之間都隔着一個微小的一半。這種想法會把人類折磨瘋,因為大家覺得有道理,聽起來好像是走不過去,但現實中你一下子就走到那兒去了,原因是什麼呢?這就是因為極限。
當你把那個圓的邊長想象成平的的時候,請問對嗎?不對吧。因為它肯定不是平的,它是個極限,所以你要抵抗一種誘惑——把極限想象成是0的誘惑。那雖然是個很小的點,但絕不是0。如果它是0,導致的結果就是整個世界會混亂。
所以大家就知道了為什麼0不能做分母。2÷0等於幾?沒這樣的題。因為2÷0等於無窮,3÷0也等於無窮,10÷0也等於無窮,那結論是什麼?2=3=10,全等於,全世界都一樣,這很明顯是錯的。所以除數為0會召喚出無窮,這個無窮就會導致整個世界的邏輯混亂,就意味着這個杯子跟桌子是相等的,因為它們除以0都一樣。所以我古人不敢召喚出無窮,因為覺得無窮是一個很難駕馭的東西。
微積分的發展
21世紀,微積分常被視為關於變化的數學,它運用了兩大概念來量化變化:導數和積分。人類先有積分思想,後有微分思想,為什麼呢?因為積分是誕生在幾何之上,微分是誕生在代數之上,代數比幾何要晚。我們今天學習微積分的時候,是先學微分,再學積分。因為微分簡單,就是求導;積分要反過來,積分更難,但是積分的思想更早出現。代數加幾何,就等於我們說的解析幾何。
那什麼是導數?比如這兒有一條曲線,曲線上有一條切線,這個切線的斜率就是切點的導數,切線的斜率表示的是變化率。我們在生活當中總得知道,一個東西多快?多陡?多敏感?凡是你問這樣的問題的時候,其實問的都是變化率。變化率怎麼算出來呢?唯一的辦法就是求導。
三大核心問題
微積分有三大核心問題:第一,正向問題,即已知一條曲線,求它各處切線的斜率,也就是變化率;第二,反向問題,已知一條曲線的各處斜率,求這條曲線的方程;第三,面積問題,已知一條曲線,求曲線下方的面積。
所以,微積分就是要知道切線,求方程;知道方程,求切線;知道方程,求面積。這些可以應用在醫學、建築、火箭發動機等各個方面。因為只要是變動的運算,都可以用方程和圖形來表示,這就是微積分的力量所在,這三大核心問題涉及物理、工程、金融、醫學等等。
人的大腦比較善於理解線性問題,但是非線性的東西很不容易理解。我們只有放大曲線中的圖像。比如,有條曲線,不知道曲線的變化率怎麼辦呢?把它放到足夠大,用顯微鏡看這一小段。請問,再彎曲的曲線在這一小段上拿顯微鏡去看,是不是都像是一條直線?這就是微積分的方法。然後發現看起來很奇怪的曲線,在這個點上就是一條斜線,是直的。這時候我們就容易理解了,所以這就是求導數。
這是由牛頓、萊布尼茨提出的。牛頓和萊布尼茨幫我們馴化了數學。微積分就是解決我們生活中問題的東西,包括我們晝夜的變化速率、物種的平衡等等。
牛頓和萊布尼茨
牛頓和萊布尼茨是徹底揭開了這個秘密的人,他們把之前的微積分思想徹底變成了微積分工具。「在牛頓和萊布尼茨創立微積分之後,情況發生了變化。他們各自發現並證明了一個基本定理,它能使這類問題常規化。該定理將面積與斜率聯繫起來,進而將積分與導數聯繫在一起。這個基本定理的影響力驚人,幾乎一夜之間面積問題就變得容易解決了。」
牛頓說:「並非所有方程都可以用曲線來表示,但我能在不到半刻鐘的時間內,判斷出它是否可以求積。」「牛頓的隱秘源泉就是微積分基本定理。
那如果曲線求積的問題得到了解決,會怎樣呢?「它將引起一個連鎖反應,一個接一個問題都會迎刃而解。而且我們可以用它來回答超出人類理解範圍的問題,即算出任意曲線的弧長。有了它,人們就可能算出平面上任何一個不規則形狀的面積,還可以計算球面、拋物面、瓮、桶以及其他繞過軸旋轉曲線所得到的曲面的表面積、體積、重心。
「不僅如此,某些預測問題將得到解決。只要解決了曲線求積問題,我們就可以預測出運動物體在遙遠未來的位置。比如,即使一顆行星受到的引力與我們宇宙中的引力不同,我們也能預測出某一時刻它在軌道上的位置。
從現代的角度看,面積問題旨在預測以不斷變化的速率變化的事物和與它隨時間的累積程度之間的關係。它與銀行賬戶的波動性流入和累計餘額有關;它與世界人口的增長率和地球上的淨人口數有關;它與化療藥物在患者血液中不斷變化的濃度和隨時間的累積暴露劑量有關,因為總暴露量會影響化療藥物的效果和毒性。」
面積問題之所以重要,因為它跟我們生活的方方面面都有聯繫。斜率是變化速率問題,面積是累積效果問題,就是用這樣的速度做了這麼長的時間,最後到底做了多少呢?這就是面積問題。所以在生活當中,我們不但要知道變化速率問題,也要知道累積效果問題。變化速率是微分,整個面積是積分,這就是微積分。
微積分的應用
在過去艾滋病是一個不治之症。所以大家覺得艾滋病會把地球上人口都消滅掉,因為艾滋病的潛伏期是十年。在這十年時間裡,這個人看起來一點問題都沒有,所以他就可以正常地生活和交往。十年期間他帶着病毒到處跟人交往,沒有任何問題,但時間一過很快就死,死亡率極高。
所以大家當時很恐慌,覺得艾滋病會讓人類滅亡,但是艾滋病並沒有這樣,原因是什麼呢?就是因為有一個華裔的醫學家何大一,他和數學家艾倫·佩雷爾森用微積分解決了艾滋病病毒的問題。何大一和他的搭檔,在人體當中截取了一個微小時間段中的病毒變化數,然後去計算病毒漲落的方程。
最後發現這十年時間裡,病毒並不是沒有發作,而是天天發作,但是你的白細胞和自然殺傷細胞每天都在和病毒作戰。你的白細胞的大量工作,使得病毒在你體內的數量達到了均衡,看起來是不動的,但實際上每天有大量的病毒死去,有大量病毒產生,然後你的白細胞和自然殺傷細胞有大量的損耗,所以當你用數學定義了這件事以後,你就可以給他配藥,然後就發明了雞尾酒療法。
雞尾酒療法是什麼呢?通俗點講,就是在這十年時間裡,給你的白細胞幫忙,讓你的白細胞能夠更厲害一點。所以現在艾滋病已經變成了一個慢性病,基本上它不會像過去那樣,得了就死了。只要你長期吃藥,就能夠一直活下去,這是多麼了不起的發現!而這個發現的背後,就是大量的數學公式。1996年,何大一博士被評選為《時代》周刊的年度風雲人物,這就是微積分的力量。
作者說,《獨立宣言》也是在微積分的影響之下寫出來的。《獨立宣言》的起草者傑斐遜是美國的第三任總統,傑斐遜本人是一個建築師、發明家和農場主,同時也是第三任總統和《獨立宣言》的起草者。除此之外,他還是牛頓的信徒,《獨立宣言》的開篇寫了一句話叫「我們認為有些真理不證自明」。也就是說從公理着手,然後憑着邏輯的力量,他從這些公理中推導出一系列難以迴避的問題,這就是《獨立宣言》的起草思路。而這個思路來自哪兒呢?來自牛頓寫的《自然哲學的數學原理》。
兩條平行線不會相交,這是公理;三角形兩邊之和大於第三邊,這是公理;兩點之間直線最短,這是公理。公理就是要搭建的一個聖殿底下的基礎,沿着這幾個基礎,全部都是公理和公理之間的應用和引用,從而證明出定理,然後定理如果得到認可,它就可以像公理一樣被使用,然後再去證明下一個定理。人類就是這樣一步一步地往前推進的,這就是科學的思想。
其次,飛機建模。我們生活中還面臨着很多變量。現代飛機翱翔在天空中,這是微積分創造的一個奇蹟。但情況並非一直如此,在航空業發展初期那個相對落後的年代,第一批飛行器是通過模仿鳥類和風箏,以及憑藉工程學知識和堅持不懈的試錯發明出來的。比如,萊特兄弟利用他們的自行車知識,設計出既可以在飛行過程中控制飛機,又能克服它們的內在不穩定性的三軸系統。
然而,隨着航空器變得越來越先進,運用更精湛的手段去設計它們也變得越發必要。風洞讓工程師可以在航空器不離開地面的情況下測試它們的空氣動力學性能。設計者建造的真機縮比模型,可以使工程師在無須建造昂貴的全尺寸模型的情況下,對航空器的適航性進行測試。
為了飛機可以安全的飛行,「其中涉及的數學計算可能難度極大,部分原因在於飛機的幾何結構十分複雜。飛機不像球體、風箏或者輕木滑翔機,它的形狀複雜得多,包含機翼、機身、發動機、尾翼、襟翼和起落裝置,這些組成部分都能使高速掠過飛機的氣流發生偏轉。而且,高速氣流一旦發生偏轉,就會對使它偏轉的物體施加一個力。」
「偏微分方程在這個過程當中發揮了諸多方面的作用。比如,除了計算升力和阻力之外,波音公司的應用數學家還用微積分預測了飛機以600英里的時速飛行時機翼會如何彎曲。當機翼受到升力時,升力會導致機翼向上彎曲和扭曲,工程師試圖避免的一種現象是被稱為氣動彈性顫振的危險效應,它類似於微風吹過百葉窗簾時發生的顫振。」
「在最好的情況下,機翼的這種不受歡迎的振動會造成旅途的顛簸和不適。而在最壞的情況下,這種振動會形成一個正反饋迴路:當機翼震顫時,它們會改變周圍的氣流,並使自身震顫得更厲害。眾所周知,氣動彈性顫振會損壞實驗飛機的機翼,導致結構失效和墜毀。」它抖得太厲害了以後,力量不斷地正向反饋,變得越來越大,機翼可能會斷掉。
所以,「波音公司的數學家將機翼近似分解為幾十萬個微型立方體、稜柱體和四面體,這些較為簡單的形狀扮演着基本結構單元的角色。他們先要為每個構建單元的剛度和彈性賦值,然後這些構建單元會受到臨近構建單元施加的推力和拉力。彈性理論的偏微分方程可以預測出每個構建單元會對這些力做出怎樣的反應,最終在超級計算機的幫助下,所有這些反應會被組合起來,用於預測機翼的總體振動情況」。
也就是說他不能把機翼當作一個整板,他要把機翼切成一個一個的小形狀,這些小形狀之間還要互相傳導力量,最後才能夠算出來機翼的安全承受力。所以你坐飛機的時候,不同的飛機顛簸程度是不一樣的。